Leia também: LITURGIA DA PALAVRA

Um livro perdido poderia ter mudado a história mundial. Desaparecido há mais de mil anos, o exemplar contém um registro único das ideias de um dos maiores estudiosos de todos os tempos.
Tudo começou em Siracusa, na região da Sicília, na Magna Grécia (sul da península Itálica colonizada pelos gregos), no ano de 287 a.C.. Foi quando Arquimedes, um gênio que estava séculos à frente do seu tempo, nasceu.
"Não há outro matemático na Antiguidade, nem na história, que chegue perto de Arquimedes", disse à BBC Chris Rorres, professor emérito de Matemática da Universidade Drexel da Pensilvânia, nos Estados Unidos, quando o manuscrito foi recuperado.
Arquimedes é popularmente conhecido como o homem que gritou "Eureka!" na banheira.

Ele estava tentando resolver um mistério sobre a coroa de ouro do rei.
O monarca suspeitava que o ourives que fabricou a coroa tinha misturado prata, metal mais barato, ao ouro que ele tinha fornecido para confecção do objeto.
A coroa tinha o peso certo (equivalente à quantidade de ouro fornecida pelo rei), mas como a prata é mais leve do que o ouro, a questão era: será que a coroa tinha um volume maior do que se tivesse sido fabricada em ouro maciço?
Certa vez, ao entrar na banheira para tomar banho, Arquimedes percebeu que quanto mais seu corpo ficava submerso, mais água transbordava. A partir desta observação, ele concluiu que poderia estabelecer quão grande era a coroa do rei ao imergi-la em um recipiente com água e medir a quantidade de líquido que seria deslocado.
Dizem que ele ficou tão entusiasmado com a descoberta que saiu imediatamente do banho e correu nu pelas ruas de Siracusa gritando "Eureka", que em grego significa "descobri".
 GETTY IMAGES
GETTY IMAGESInventor famoso
Não sabemos se os cidadãos da Sicília realmente viram Arquimedes nu, mas a verdade sobre a coroa do rei foi revelada: o ourives tinha sido desonesto e o matemático havia se mostrado um excelente detetive.
Durante sua vida, Arquimedes tornou-se famoso por suas invenções e temido por suas armas de guerra.
Foi também nomeado conselheiro militar pelo rei de Siracusa, que o confiou a defesa da cidade.

Mas é por meio da matemática que sua verdadeira genialidade aparece. Foi ele que considerou estimar um valor para π (Pi), vital para calcular a área de um círculo, um dos componentes básicos da ciência.
Ele fez isso colocando um círculo entre polígonos, já que seu perímetro pode ser calculado, pois seus lados são retos.
Ele começou inserindo um hexágono dentro do círculo e outro fora. Em seguida, foi adicionando mais e mais lados até chegar a 96.
A ideia era fazer com que os polígonos se aproximassem o máximo possível do perímetro do círculo, o que lhe daria os limites cada vez mais próximos entre os quais deveria estar π.
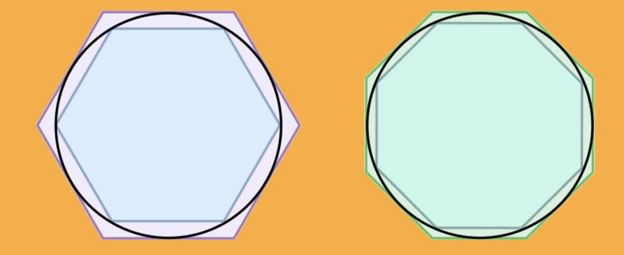
Ele calculou assim que o valor de π estava entre 310/71 (aproximadamente 3.1408) e 31/7 (cerca de 3.1429), uma estimativa que ainda é usada pelos engenheiros hoje - e é mais do que suficiente para todos os propósitos práticos.
Obcecado por matemática, o estudioso não enxergava nenhum problema como difícil demais.
Ele chegou a tentar, inclusive, calcular a quantidade de grãos de areia necessários para preencher todo o Universo.
A resposta: 10, seguido de 62 zeros.
Os historiadores da época contam que Arquimedes ficava eufórico quando descobria formas matemáticas cada vez mais complexas.
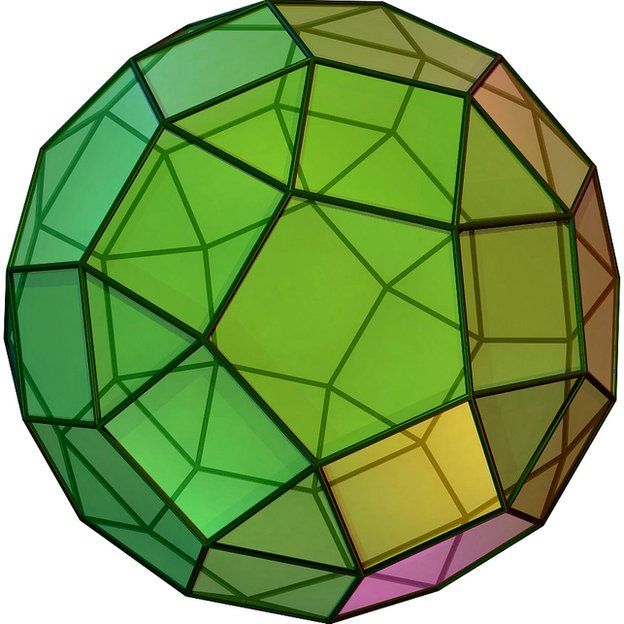
4 triângulos e 4 hexágonos formam um tetraedro truncado ...
12 quadrados, 8 hexágonos, 6 octágonos - octaedro truncado ...
12 pentágonos, 30 quadrados e 20 triângulos, 60 vértices, 120 arestas, 62 faces: um rombicuboctaedro.
Basta!
Tragicamente, Arquimedes ficou tão conhecido que até os romanos sabiam da sua existência e desejavam capturá-lo.
Quando finalmente conseguiram invadir a cidade de Siracusa, deram ordem para prendê-lo. Mas o soldado que o encontrou se distraiu e, sem notar a confusão ao seu redor, não recebeu as instruções corretas. Por isso, matou-o com a espada.

Uma reciclagem devastadora
A morte de Arquimedes, em 212 a.C., marcou o fim de uma era de ouro na matemática grega, que foi declinando gradualmente.
No entanto, seus manuscritos sobreviveram, sendo reproduzidos por escribas que transmitiram seus conhecimentos de geração para geração. No século 10, foi produzida uma cópia final de suas obras mais importantes.
Mas o interesse pela matemática havia se perdido, e o nome de Arquimedes foi esquecido.

Certo dia, no século 12, um monge ficou sem pergaminhos. A consequência disso foi desastrosa.
As páginas da cópia final da obra mais importante de Arquimedes foram reutilizadas para fazer um livro de orações.
Cada uma das folhas que formavam uma página dupla do manuscrito foram cortadas e dobradas para dar origem a novas páginas, que, após serem lavadas e raspadas, ficaram suficientemente claras para se escrever novamente sobre elas.
O manuscrito foi reciclado e transformado em um palimpsesto - um papiro ou pergaminho que "mais uma vez" (palin, em grego) foi "raspado" (em grego, psao) para apagar o que estava escrito e ser reutilizado.
Tornou-se, assim, um livro de orações do mosteiro de Mar Saba, no deserto da Judeia, no Oriente Médio.
O renascimento matemático
No século 15, o Renascimento chegou à Europa. A ciência avançou o suficiente para que os estudiosos compreendessem os argumentos matemáticos de Arquimedes.
No entanto, ninguém tinha noção que algumas de suas maiores ideias haviam se perdido.

Os matemáticos renascentistas tiveram que lidar com conceitos e problemas que Arquimedes havia resolvido 1,5 mil anos antes.
Mas centenas de anos se passaram até que o manuscrito do grego viesse à tona novamente. Ninguém sabe como, mas ele apareceu em uma biblioteca de Constantinopla, atual cidade turca de Istambul.
Em 1906, ao revisar o catálogo da biblioteca, Johan Ludvig Heiberg, especialista dinamarquês em cultura grega, se deparou com algo no documento que despertou sua curiosidade.

"Ele deve ter ficado atordoado ao ver o manuscrito. Ele sabia muito bem o quão valioso era o que ele estava lendo", afirmou à BBC William Noel, ex-curador do Museu de Arte Walters, nos EUA. Atualmente, ele é diretor do Instituto Schoenberg para Estudos de Manuscritos da Penn Libraries, na Filadélfia.
Como não podia retirar o manuscrito da biblioteca, Heiberg tirou fotos das páginas e, com base nelas, tentou reconstruir o trabalho de Arquimedes, uma tarefa incrivelmente árdua quando sua única aliada era uma lupa.
De qualquer forma, a descoberta de Heiberg revelou ideias que até então não eram conhecidas.
No livro, Arquimedes não só dava as respostas para seus cálculos, como tinha escrito seus pensamentos mais íntimos, revelando como tinha feito seu trabalho.
'O Método'
"Foi uma descoberta espetacular para a história da matemática. Se você é pintor, provavelmente tem interesse nas obras finalizadas dos grandes mestres da pintura. Mas, além disso, você quer saber as técnicas, os métodos, as tintas que eles usaram. Os matemáticos querem saber não apenas quais são seus teoremas, mas como se chegou até eles ", compara Rorres.
O Método, título dado à obra, mostrou que Arquimedes criou uma abordagem radical que nenhum matemático havia chegado perto de inventar.

Em sua mente, ele havia construído um conjunto de escalas completamente imaginárias para comparar os volumes de formas curvas - o que ele usou para tentar calcular o volume de uma esfera.
Como já se conhecia o volume de um cone e de um cilindro, ele tentava equilibrar a esfera e o cone de um lado com o cilindro no outro. Tudo isso mentalmente.
Arquimedes imaginou um número infinito de cortes e, usando uma matemática muito complexa, encontrou uma maneira de equilibrar os objetos nas escalas.
O resultado final: o volume de uma esfera é precisamente dois terços do volume do cilindro que encerra essa esfera.
O matemático considerava a descoberta tão importante que pediu que fosse inscrita em sua lápide.
Ao arquitetar volumes usando cortes infinitos, Arquimedes dava o primeiro passo em direção a um ramo vital da matemática, conhecido como cálculo, 1,8 mil anos antes de ser inventado.

O mundo moderno não poderia existir sem o cálculo - é essencial para cientistas e engenheiros, e a tecnologia do século 21 depende disso.
Outro desaparecimento
Em 1914, quando estava prestes a descobrir a verdadeira genialidade de Arquimedes, o plano de Heiberg de estudar o manuscrito em Constantinopla foi bruscamente interrompido.
Com o início da Primeira Guerra Mundial (1914-1918), a Europa e o Oriente Médio foram tomados pelo caos, e o palimpsesto onde estavam os escritos do matemático se perdeu novamente.
Os acadêmicos tinham poucas esperanças de reaver o documento, mas, em 1971, Nigel Wilson, um especialista em Grécia antiga, ouviu falar de uma página de um manuscrito em uma biblioteca da Universidade de Cambridge, no Reino Unido, e foi investigar.
"Transcrevi algumas frases. Havia termos técnicos muito específicos. Pelo vocabulário, descobri rapidamente que se tratava de um ensaio de Arquimedes, e me dei conta que deveria ser uma folha do famoso palimpsesto", disse à BBC Wilson, professor de Estudos Clássicos da Universidade de Oxford.
Mas por que apenas uma página do palimpsesto de Arquimedes foi parar em Cambridge?

Uma pista era sua procedência: uma coleção de documentos que pertencia a um erudito chamado Constantine Tischendorf, um homem de poucos escrúpulos.
"Tischendorf viajou muito pelo Oriente Médio. Em Constantinopla, visitou a biblioteca e disse que havia apenas um manuscrito de seu interesse: um palimpsesto com um texto matemático. Não disse mais nada", contou Wilson.
"Não podemos deixar de supor que essa página foi roubada", acrescenta.
No início do século 20, Heiberg contava só com uma lupa para ler o manuscrito. Nos anos 1970, Nigel Wilson tinha a seu favor a tecnologia moderna.
"A maior parte da página era legível e, com a lâmpada ultravioleta, os cantos, que não podiam ser lidos, ficaram nítidos."

Após a 1ª Guerra Mundial, Paris e outras cidades europeias foram inundadas de obras de arte do Oriente Médio, mas ninguém tinha visto o documento de Arquimedes.
Em 1991, Felix de Marez Oyens começou a trabalhar para a casa de leilões Christie's e, em seu novo escritório, encontrou a carta de uma família francesa que dizia ter um palimpsesto.
Intrigado, De Marez Oyens foi examinar o livro. "De cara eu soube que deveria ser o manuscrito que Heiberg estudou pela primeira vez em 1906", disse à BBC De Marez Oyens.
Os proprietários contaram que, na década de 1920, um parente que era colecionador amador havia adquirido o manuscrito em Constantinopla. Agora eles queriam vendê-lo.
Mas qual é o preço de algo inestimável?
"Qualquer avaliação de algo assim é simplesmente uma suposição. Acho que eu disse a eles que valia entre US$ 550 mil e US$ 800 mil", afirmou De Marez Oyens.
O manuscrito foi vendido por muito mais. Um bilionário anônimo pagou US$ 2 milhões.
Em 1998, era chegada finalmente a hora de recuperar o conhecimento perdido por mais de dois milênios. Alguns meses após comprar o manuscrito, o novo dono entregou o documento ao Museu de Arte Walters, em Baltimore, no estado de Maryland, nos EUA.
Cientistas, restauradores e historiadores começaram a se debruçar sobre a obra.

Usando tecnologia de imagem multiespectral e uma técnica de raio-X que faz brilhar o ferro da tinta que foi raspada, eles descobriram que o documento continha não só sete tratados de Arquimedes, como também discursos de Hipérides, político e orador ateniense, e comentários sobre as categorias de Aristóteles do século 2 ou 3.
Entre os tratados do matemático grego, estava a única cópia sobrevivente do Stomachion de Arquimedes, no qual ele tenta descobrir de quantas maneiras é possível combinar 14 peças fixas para formar um quadrado perfeito.

A resposta é 17.152 combinações.
Stomachion significa dor de estômago, que é como se referiam aos enigmas na antiguidade.
Trata-se do primeiro trabalho a desenvolver a matemática das combinações, que é a base da probabilidade, algo que se acreditava ter surgido nos séculos 17 ou 18.
Até o infinito
Sem dúvida, a leitura de O Método deixou claro que Arquimedes deu um grande passo para a compreensão do infinito; mais que isso, usou o conceito como parte do argumento de um de seus teoremas.
Arquimedes estava mais próximo da ciência moderna do que se imaginava. Embora se soubesse que ele tinha dado alguns passos na direção do cálculo moderno, o palimpsesto mostrou que, de certa forma, o grego já havia chegado lá.

O que teria acontecido, então, se esse documento não tivesse sido perdido? Se os matemáticos do Renascimento tivessem tido acesso a ele?
"Isso teria mudado a matemática, é claro, mas devemos ter em mente que influenciaria todas as ciências. Então, basicamente, teria sido se a maré do conhecimento tivesse subido centenas de anos atrás", responde Rorres.
Fonte http://www.bbc.com/portuguese/geral-42494730

Nenhum comentário:
Postar um comentário